本期为大家搬运来了在UE学习中需要注意的数学基础知识。掌握好这些数学基础有助于在UE4学习中获得更好的成长道路。

开个坑，描述也许不是很准确：美术必备的数学基础知识系列。内容面向小白，非常初级，希望能讲明白，如果有表达错误或者不准确的地方欢迎指正。

内容示例工程是学习UE4很方便的工具，但是很多人并没有在意或者在工程里摸不着头脑不知从何下手，这个系列会从Math Hall着手，带你跟着示例一个节点一个节点地漫游数学殿堂。

本篇作为预备知识，与示例工程没多大关系。美术出身的你，想要掌握UE4的材质系统，甚至想在TA方向上走下去，SD也好，其他引擎也好，本篇可以作为你开始这个旅途的起点，分四步颠覆掉你对贴图的认知，开始学会用数学的思维看待它。

1、通道

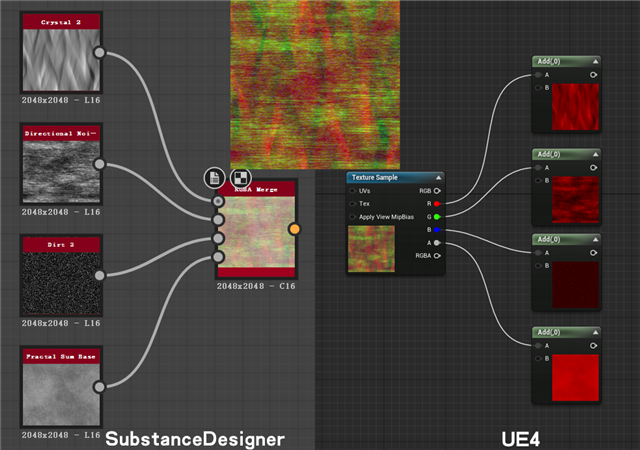
首先最基本的，我们知道一张图片通常有RGBA四个通道，而很多情况下我们需要的是一张灰度图，比如Roughness、Metallic、Height等等以及一些遮罩，噪波。这时候如果每个灰度图都存成一个图片文件就会比较浪费，所以我们会选择多个灰度图分别放到一张图片的不同通道中打包储存，调用时只要读取相应的通道。

这时候的你见到的这张帖图，是个可以存4张灰度图的打包文件。

2、每个像素都是数字

众所周知，一张图的每个像素都有一个RGB值，所以加上Alpha通道，每个像素都可以保存4个数字。作为美术的你看到的是一张图片，但换上数学思维，它可以是一个矩阵。比如一张2X2的图，你需要意识到它也是一个2X2的矩阵。

对图片的处理，其实就是对图片中每个像素的RGB数值进行的数学运算。

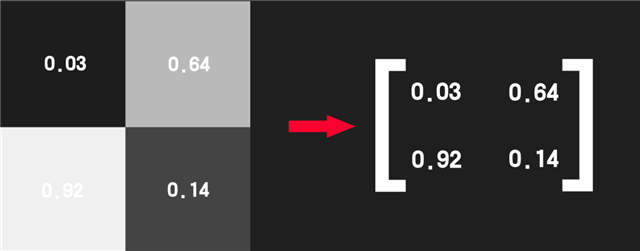
单个通道的四个像素组成的矩阵

3、坐标系

既然每个通道我们可以在0-1的范围内取值，那我们就可以得到一个0-1范围的数轴，用两个通道建立一个二维坐标系（直角坐标系），用三个通道建立一个三维坐标系。

通常我们用RGB三个通道分别代表XYZ三个轴向上的数值。在二维坐标系中，尝试取图片最左上角作为（0，0）点，X轴向右延申，Y轴向下延申，分别把XY的数值所对应的色值填充到坐标系中，然后把X轴与Y轴分别作为R通道和G通道叠加在一起，你就会瞬间理解为什么UE4中处理UV的Texcoord缩略图是长这样的以及它为什么叫Texcoord了（Texture Coordinates）

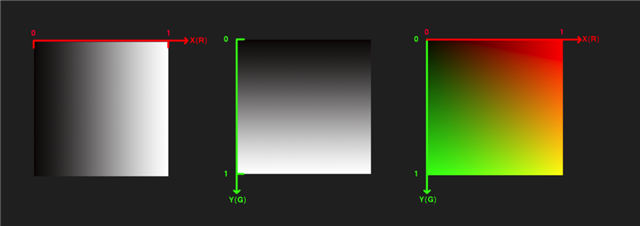
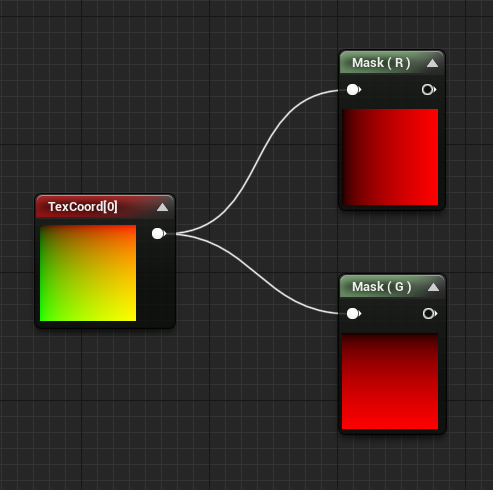
顺带一提，所以我们可以通过只读取Texcoord的R通道或者G通道来得到一个线性渐变。

相信现在你也能理解，法线贴图为什么长这样了：

它就是用三个通道分别储存了XYZ三个轴向的信息。

4、位置和向量

有了坐标系，我们就可以在图片中记录对象在空间中的位置，同样顺理成章地我们可以引入向量。

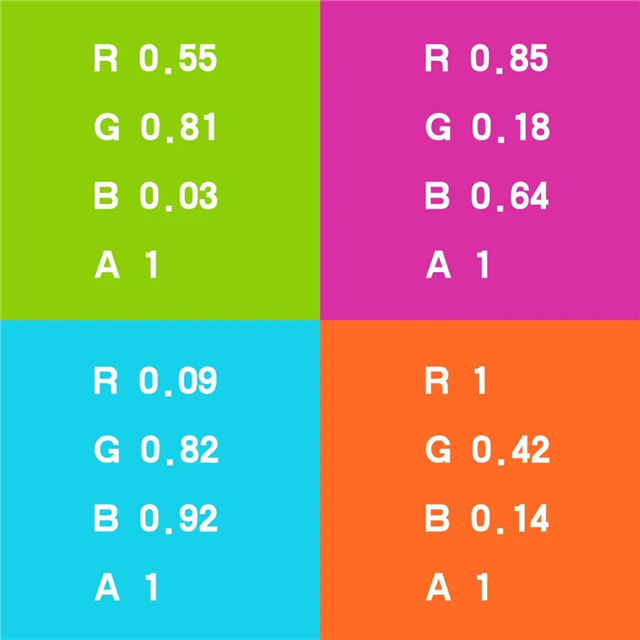
这是一张2X2像素放大之后的图

上面这张2X2像素的图，忽略alpha通道，只看RGB通道，我们可以认为它储存了4个三维空间的位置坐标，把这4个点作为向量终点，我们就得到了4个起点位于坐标原点的向量。

上面那张图里4个像素可以告诉我们的信息

既然每个像素都可以储存一个位置信息，那么把一张图从左上角开始给每个像素依次编号，计算机按顺序读取每个像素的RGB值，这张图就可以用于储存动画信息了。

如果我们把RGB值看作向量，那一张图就可以储存任何带有方向性的参数，比如速度、加速度、力等等，于是图片也可以储存场信息了。

每个向量都是一个像素

以上并不是贴图可以储存的全部信息，但是足够可以帮大家打开思维，比如UE4中，可以用一张图的一行像素储存一条曲线。

相信现在你对贴图已经有了全新的认知，下一篇开始我们一起逛逛UE4里的数学殿堂吧。